Paradoxes of the Second Law
The Big Bang had maximum disorder, and disorder has only increased since then.
Start with the idea that physics can’t explain the simple fact of our different relationships to the past and the future. The prevailing scientific paradigm is “reductionism”, which says that physics on the smallest scale gives rise to chemistry, biology, and everything that we see on the largest scales. But the laws of physics on the smallest scales are time-symmetric. There is no difference between forward time and reverse time in any of the laws of fundamental physics. This is a paradox which has never been resolved by the soaring intelligences thinking about the foundations of physics. Much has been written; little has been agreed. So physicists do the practical thing: they think in terms of the past causing the future, and set up their equations to discover how. They never run the same equations to see how the future can cause the past.
The Second Law of Thermodynamics says that entropy is always increasing. The universe moves, from moment to moment, always into a more disordered state. Order is dissipating. Energy remains constant, but the capacity of that energy to do anything useful or interesting is diminishing, as more and more of the energy takes the form of heat, the heat spreads uniformly through all matter, and the matter spreads uniformly through space. Boringer and boringer.
The Big Bang began in a state of uniformly high temperature, an undifferentiated distribution of plasma and enough radiation to be in equilibrium with the matter. There was no structure. There was zero information. The universe was in a state of maximum entropy — that, in fact, is the definition of “thermodynamic equilibrium”.
Over the next 13 billion years, the entropy went up and up — as it must according to the Second Law of Thermodynamics. Entropy is the physicists’ measure of disorder, so disorder increased continually from a time when it was already at a maximum. And the result was a universe of many interesting structures — stars, galaxies, planets, dust clouds, quasars, black holes and Life — and the Second Law assures us that the disorder is now at a higher level than those first minutes when entropy was at a maximum. The universe has grown interestinger and interestinger.
Starting from a state of maximum entropy, and entropy increases from there? Starting with no order or structure and developing stars and galaxies over time? How could this be consistent with the Second Law?
Expansion
The first step in explaining this paradox is to consider that the universe is expanding. You know that gas will expand into a vacuum. So it’s not surprising to learn that entropy is greater if the gas is spread out over a large space than if it is all compressed in a small space, with another empty space alongside it.
As the universe expands, there is an opportunity for entropy to increase. This is true even though, when the universe was smaller, there was no “empty space” outside it. The space itself expands.** So, in the first minute of the Big Bang, entropy was at the maximum value available to a small universe, and as the universe grew, the maximum possible entropy grew with it.
Even though the matter started out as random as it could possibly be, as the universe expands, there are more places to occupy, and thus opportunity for ever greater randomness. Can the matter keep up with the pace of expansion and always remain in the most random possible state? Luckily, it cannot.†
During those first few minutes, the temperature of the universe was comparable to the center of the sun, and there was a chance for hydrogen to fuse into deuterium (heavy hydrogen) and into helium, and even into heavier elements. But the expansion happened faster than the fusion could keep up. A quarter of the hydrogen turned into helium. A tiny amount was stranded mid-stream as deuterium. Three quarters remained in the form of hydrogen.
The formation of helium during the first three minutes of the universe was the subject of a speculation that launched the career of young George Gamow. In a calculation (published 1948) with his PhD advisor, Ralph Alpher, Gamow showed that if the Big Bang were hot enough bur not too hot, it could explain the observed fact that the universe seemed to be about ¾ hydrogen and ¼ helium. If the universe really was this hot, they predicted that the leftover radiation should have cooled all the way down from billions of degrees to just a few degrees above absolute zero, but might be observable as thermal radio waves coming from every direction in space. This radiation was actually detected 17 years later by Penzias and Wilson from a radio telescope in Princeton. The existence of this ubiquitous background radiation is the strongest evidence we have for the Big Bang theory.
As a joke, the two of them asked world-renowned physicist Hans Bethe to add his name to the author list. (All three of them were in the Cornell physics department.) So the paper was signed by Alpher, Bethe, and Gamow, which sounds a lot like the first three letters of the Greek alphabet. It was published on April first.
Nobel physicist Stephen Weinberg wrote a readable account of nuclear reactions in The First Three Minutes.
Definitions
Entropy is roughly “randomness”, and it has a quantitative definition which we take from Ludwig Boltzmann’s gravestone. We see an object from the outside, and can measure its macroscopic dimensions, size and shape, and other macroscopic things like its chemical composition, its temperature, and its pressure. But inside, there are different ways that the atoms can be configured that all look the same from a macroscopic perspective. Imagine counting up the number of ways that the atoms can be configured that all correspond to the same system as viewed from the outside on a macroscopic scale. The number of atoms is huge and the number of ways they can be rearranged such that we on the outside would be none the wiser is yet more huge. The log function can rein in a really huge number and make it more manageable. Boltzmann defined entropy as the log of the number of atomic-scale configurations that correspond to the same human-scale view of any object or collection of objects.
Boltzmann’s grave stone
Free Energy is the amount of energy in a system over and above the amount that is distributed randomly. The free energy can potentially be harnessed in a machine to do work, but the residual random energy is useless. Free energy is a rigorously-defined quantity in terms of the total energy and the entropy. It is simply energy minus temperature times entropy.
In thermodynamic equilibrium, there is energy, but no free energy. Entropy attains its maximum value, and no energy is available that we can harness to do useful work.
Temperature is related to the amount of energy in a system divided by the number of particles in the system.†† The energy tends to distribute itself over the particles in a particular way, and that corresponds to thermodynamic equilibrium. Most of the particles have just about their fair share of the energy, plus or minus, and the number of particles that have much more energy than their share become exponentially rare for much higher energies or much lower energies. A system that is not in thermodynamic equilibrium can’t really be characterized as having a single temperature.
We take it for granted that temperature is a meaningful idea. For example, when we set the thermostat for 70 degrees, the furniture and the walls and the air will all come to 70 degrees and they won’t “fight with each other” over heat. It could have been otherwise. Different materials store heat in different ways, so that it could be that
the air and the walls would stop exchanging heat between them
the air and the couch would stop exchanging heat between them
but if you put the couch in contact with the wall, heat would flow from couch to wall.
If A is the same temperature as B, and B is the same temperature as C, then A is the same temperature as C. If this were not true, then temperature would not be a useful concept. And yet, there is no reason why it has to be true. It is true that temperature is a meaningful concept most of the time, but paradoxes can arise when A=B and B=C but A≠C. Daniel Sheehan discovered an example of this that I wrote about last year.
Galaxies and Stars
The existence of this hydrogen, frozen in its primordial state, explains a lot. Stars like our sun are powered by fusing hydrogen into helium — finishing the job that was only ¼ complete in the first few minutes. In fact, the vast majority of that hydrogen left over from the Big Bang is still available and unused after 13 billion years.
Fusing hydrogen to helium produces the sunlight that keeps the earth warm. Sunlight is also the ultimate source of almost all the chemical energy that drives life on earth. (Almost because there is some life deep in the ocean that draws energy from chemicals that bubble into the oceans from rocks below.)
In addition to energy from nuclear fusion, there is energy from gravity. Gravity provides the energy that makes the galactic pinwheel spin and makes the earth revolve around the sun. Gravity also generated the heat that kickstarted the nuclear fusion at the center of the sun 5 billion years ago. But where was the gravitational energy in those first few moments of the Big Bang? Was the gas really in its highest entropy state or would a giant black hole have had even higher entropy?
It is not obvious how to incorporate gravity into the Second Law, and physicists have worked on this question for the last half century. Next week, I’ll write about paradoxes associated with gravity and the Second Law.
Aging and Life
Living things have acquired a talent for collecting free energy and using it to build up their bodies, to run their metabolisms, to move and to grow. The free energy may come in the form of sunlight (green plants) or chemical energy (everything else). The chemicals are returned to the environment as waste products that have lower energy content than what was consumed; and the energy is returned to the environment as low-grade warmth.
Thus living things are able to accumulate order and structure in themselves, at the expense of their environment. Living things gather free energy from the environment, dump their entropy back into the environment, and pocket the difference in the form of growth, movement, perception, metabolism, and all the other functions of a living organism.
Living things don’t violate the Second Law. They are dependent on external sources of free energy.
There is a common misconception — even among some biologists and physicists who should know better — that the reason for aging and death is the Second Law of Thermodynamics. The truth is that there is no physical necessity for aging. Any living thing could go on growing and accumulating more order, more free energy in its body, year after year. The oldest living thing presently on the planet is an aspen grove, grown from a single seed eighty thousand years ago. It will go on until something kills it. It will not die of old age, and as far as the Second Law is concerned, neither should we. It would be physically possible for a human, like the aspen grove, to keep on living until something kills us. Aging is a function of biology, not of physics.
OK for now — but bigger paradoxes to come
The universe started in a state of maximum entropy with no structure,, and now it is in a state of even higher entropy — but it has a great deal of structure. This seems paradoxical, but there is good agreement among physicists that it can be explained by expansion of the universe. The maximum possible entropy grows with the expansion, and the progression toward more entropy hasn’t kept up with the growing possibilities. In particular, ¾ of the hydrogen in the universe didn’t get fused into helium, and that hydrogen has fueled all the stars in all the galaxies for 13 billion years, with only another 1% of the hydrogen used up so far.
This story was laid out in a journal article by Stephen Hawking in 1985. David Layzer wrote a Scientific American article explaining it in less technical terms, and adding his own twist. (Layzer was my teacher when I was a young Harvard student, already interested in the paradoxes of time.)
So far so good.
But we haven’t yet taken gravity into account. The energy that is potentially available when matter clusters together is even greater than the energy that is released when hydrogen fuses into helium. In fact, as stars collapse toward black holes, the helium can come apart into hydrogen again.
So you might think, “Gravity is king. In the end, gravity is the source of all the free energy in the universe and all the departure from pure randomness.” But in the long, long run, even gravity yields to quantum randomness and black holes evaporate into a state of uniformly distributed radiation. That sounds a lot like the original state of the Big Bang.
Unless the universe has enough mass density so that the the expansion is halted one day by gravity and the universal expansion becomes a universal contraction for billions of years more. What would happen then? Some physicists say the Second Law will be reversed, and entropy will begin decreasing in the collapse phase. Will scientists in that world see broken glass that re-assemble itself into perfect crystal goblets, and fried eggs un-frying, ultimately to be sucked up into a chicken? Or will they experience time just as we do because their future will feel like the past to them? Maybe the “second half people” are really us, and we’re really in a collapsing universe that feels to us as though it is expanding.
The paradoxes are yet to come, and I will write more next week.





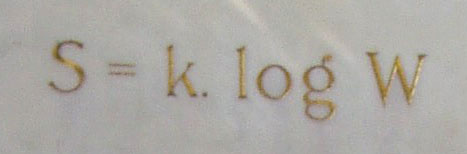
In my humble opinion, the Universe has always existed and always will exist. If there was a "Big Bang" (or more than one), then it (or they) expanded into the infinite Universe.
I also suspect that life has always existed in some form in one or more parts of the Universe. Life itself may by the counter to the alleged "Heat Death of the Universe" when Entropy has its final say.