Computer models are the mainstay of modern science. They comprise the lion’s share of the explosion of scientific literature in the 21st Century.
Analytic Solutions yield to Computer Models
Before computer models, quantitative science was limited to the simplest systems, those that could be described by a few equations and for which the equations happened to have analytic solutions*. This led to distortions of science. Since science is a very human endeavor, practicing scientists behaved like the drunk looking for his keys under the lamppost. We spent all our time on the systems of equations that we could solve (by hand, on paper), and this led to the illusion that the tiny corner of nature we were able to illuminate in this way was representative of the rest. It wasn’t.
An example close to my work is the selfish gene theory, based on the model introduced by R. A. Fisher in the 1920s. Fisher proposed the first quantitative theory of Darwinian selection, which became ensconced as a standard in evolutionary theory, called “Population Genetics” or the “New Synthesis” (the latter referring to a synthesis of Darwin’s selection with Mendel’s genetics). Fisher’s theory painted a highly distorted picture of the way nature works, because it predicted that only selfishness, and not cooperation, has any selective value.
For decades, Fisher’s model was mistaken for reality. The best and brightest of evolutionary theorists, notably John Maynard Smith and George Williams, argued that selfish strategies were much more efficient and more rapid than cooperative strategies, so cooperation could never evolve. But their argument was based only on theory, and neglected the diverse and ubiquitous examples of cooperation that we see in nature. Worse, they took Fisher’s simple model as being the one true theory of how evolution works. They argued that his mathematics constituted a rigorous proof that natural selection would almost never prefer cooperation to selfishness.
Computer technology advanced. In 1975, the first computer models of evolutionary ecology were feasible, but only in the 21st century did they became common. (This is a literature to which I personally contributed, beginning in 2000.) There is now abundant computational support for understanding how cooperation has become a prevalent theme of behavioral ecology.
Computer Models yield to ??
My punch line is this: Computer models also have their limitations, and just as 20th Century science was looking for solutions under the lamppost of algebraic formulas that they could write down, 21st Century science is currently limited by the lamppost of computer models. The problem is that the two most fundamental theories in science, Quantum Mechanics and General Relativity, are so absurdly complex in their general cases, that they cannot be modeled by present-day computers, nor by any computer we can now conceive.
General Relativity
Einstein’s GR equation describes how matter/energy bends space in its vicinity. It is usually written in this form:
It doesn’t look so complicated, but that is because the notation masks an unfathomable amount of computation. The left side is the curvature of space. G is a curvature tensor and the subscripts μ and ν represent 3 dimensions of space and one of time. So Gμν represents a tensor of 16 numbers, but worse than this it can only be computed by first computing the full curvature tensor, Gμνσλ, which has 64 components. The second term on the left represents a constant curvature everywhere in space, corresponding to dark energy, which (according to current theory and observations), is important on the largest scales in the universe.
The term on the right is a constant, 8πG/c^4, times another tensor that represents mass, energy and momentum, wherever they appear in space. (The G on the right has nothing to do with the G on the left. This constant G is the not a tensor; it is just a number, the same gravitational constant in Newton’s gravity. I apologize for bad notation, but this is the convention.)
How to use these 16 equations? If we’re used to classical physics from Newton’s equations, we might think in terms of starting with the distribution of matter that we know (the right side), then computing the field (on the left side) and from the field, computing how the matter will change its motion (accelerate), affecting the future position, which we might feed back into the right side. This, in practice, is the way dynamic computer models are constructed. But in GR, there is only this one equation, describing both how matter/energy produces fields and how fields govern the movement of matter/energy. We can’t use one side to solve for the other, but must search for self-consistent solutions.
There are mathematical techniques for finding such solutions, but the catch-22 of the GR equation is that there are so many interlocked equations. The full 64 components of the curvature tensor are needed to determine how matter responds, so the simple appearance of this equation is illusory. In the general case, one must solve 64 linked non-linear partial differential equations in 64 unknowns. No computer in the foreseeable future could tackle this problem.
Currently, there is a science of computational relativity. People are generating solutions to Einstein’s field equations, but only for the simplest cases where there is either extreme symmetry or weak fields. If the fields are weak, Einstein’s complicated equations reduce to Newton’s simple ones. If there is extreme symmetry, the 64 linked equations can be reduced to one or two.
The standard way to compute models of the universe based on the Big Bang assumes that the universe is perfectly homogeneous. Everything is the same everywhere, and it is only the expansion (and consequent dilution) through time that must be computed.
Ever since 1917 when Einstein first published these field equations, cosmologists have been computing models of the universe based on the assumption that everything is the same everywhere. For awhile, it appeared that these models were able to explain astronomical observations in general, including the abundance of different elements and the 3 degree blackbody background. But in the last 25 years, there has been an unfolding crisis in cosmology, as it became clear that theory and observations don’t match. The standard kluge has been to introduce “dark energy” and “dark matter” into the model, even though no one has ever observed either, and we have no idea what they might be. The situation is not satisfying. Worse than this, there is mounting observational evidence in recent years that the universe is not homogeneous. We may take comfort from the fact that this means there is no mismatch, no requirement for dark matter or dark energy. Or we may despair that we don’t know how to compute anything in cosmology once we face the full complexity of Einstein’s 64 linked, non-linear partial differential equations in 64 unknowns. (That’s the situation when we give up the idea that the universe is homogeneous.)
Quantum Mechanics
Quantum mechanics presents equations that are even more intractable than Einstein’s field equations. Mathematicians haven’t a clue how to approach them.
The issue is that, in QM, the equation for N separate particles cannot be separated into N separate equations. It is this separation that allows us to compute solutions to classical Newtonian equations for many particles.
Technically: In the Newtonian case, we typically start with positions and velocities of N particles at some initial time. We use the positions of the particles to compute fields (gravitational, electric, etc) and use the fields to compute the change in velocities for all N particles. Then we recreate the system a small time Δt later by moving the particles according to their respective velocities and updating their velocities according to the computed accelerations. Repeating this procedure advances the system gradually, Δt forward with each iteraion. Using this technique, we can calculate the motion of any system of N particles, and it takes N times as long as if we had just one particle to calculate.
The reason we can’t do this in QM is because of entanglement. You’ve heard that word—it’s the way that everything in QM is connected to everything else. In QM, not only are the particles’ motions mutually interdependent (which is the kind of mathematical issue we ran into in GR), but we can no longer even think in terms of N wave functions evolving in 3-space. QM dictates that we have to describe a “configuration” or a situation, comprising all N particles. Our wave function is a single function that lives in a 3N-dimensional space. So the number of computations we need grows exponentially with N, not linearly as in the Newtonian case.
This is a disaster for computing how a system evolves whenever N gets large. Typically, we might want to map a wave function in space by dividing space into 1,000 small units in each dimension. So a single particle wave function requires us to map a function on a grid 1,000*1,000*1,000 pixels. That’s not bad at all — today’s computers can easily manipulate 1 billion values. But for N=2, there are a billion billion (10^18) values to keep track of and follow and update. That is on the edge of what can be done with today’s computers, using tricks to simplify the problem. And N=3 particles, with 10^27 moving parts is beyond possibility. A gigaflops computer (10^12 operations per second) would need about a million years to calculate each Δt. And N=4 particles is utterly hopeless. For reference, a single water molecule has N=10 electrons, and a typical biomolecule has several thousand electrons.
(Technical note: The first particle is free. Two particles really corresponds to N=1, since there is a mathematical trick by which all motions can be related to the center of mass. This means that quantum physicists can compute in detail a 2-particle collision with relative ease. All the computations of what particles come out of a particle accelerator come in this category. But a 3-particle situation (for example, a He atom or a molecule of H2) becomes a billion times harder, and that is today’s state-of-the-art. We can’t compute the wave function for anything more complicated.)
In practice, quantum mechanical calculations are limited to very small numbers of particles or large systems where all the particles are doing the same thing. In a laser, there is one wave function for many trillions of photons, or more. In solid state physics, there are various tricks and approximations used, all based on separating (approximately) the wave functions for each electron. QM computations involving molecules are not performed from first principles, but based on measured properties of the molecules, together with even cruder approximations.
Applications
This is why we don’t have a predictive science of chemical or biological systems, not even an idea about how to build one. Quantum teleportation of macroscopic objects would require measuring and codifying a ridiculous number of quantum parameters, even if there were no entanglement and it could be done with separate particles. Since particles are entangled, this idea is a non-starter. Similarly, the idea of “uploading our brain state to a computer” can only make sense to someone who doesn’t understand entanglement**. (Perhaps these people imagine that a biological cell can be understood in terms of bulk chemistry, rather than a wave state of 10^17 entangled molecules.)
Most ridiculous is the speculation that we live in a simulation. As I showed above, full simulation of a water molecule is utterly intractable. Only people who don’t understand this can talk about simulation of a planet or a universe.
Quantum computers to the rescue?
Quantum systems move forward in time by computing their future from their present far more efficiently than a computer can. At present, we know only how to solve a few types of problems on a quantum computer. But if ever we figure out how to build a general-purpose quantum computer, the absolute limit is that it will be able to simulate a system no faster than the system “simulates itself”. In other words, full quantum simulations will always be slower than simply doing an experiment on a quantum system, and watching how it evolves over time.
I’m an optimist
I savor the mystery of questions that are beyond our present science. I don’t give up pushing the limits. The more thought we put into these difficult problems, the deeper is our sense of wonder when contemplating the questions that are beyond our science. Even our failures offer uplifting messages.
But I don’t cast Science in the role of Sysiphus, who must find consolation in an eternity of failure. I do believe that new understandings will come about concerning fundamental issues like the large-scale structure of the Universe and the relationship between mind and brain. But these new understandings will not come from better and faster computers, or from incremental advances in science. Science will need conceptual frameworks that are outside anything we now imagine.
—————————
* An “analytic solution” simply means a formula that can be written as a combination of familiar functions, like y=x^2, or f(x,y,z) = sin(x)*e^(-3y) + √z. You might think that any function could be written as a combination like this, and you would be wrong. There is indeed an infinity of such functions, but there is a much larger infinity of functions that have no representation like this in terms of familiar primitives.
** From my perspective, another problem with “uploading my brain state” is that I don’t believe that the brain creates consciousness. I believe mind is a non-physical entity, and that “consciousness is the ground of all being” [Amit Goswami]. William James (1898) articulated this position with his usual clarity.



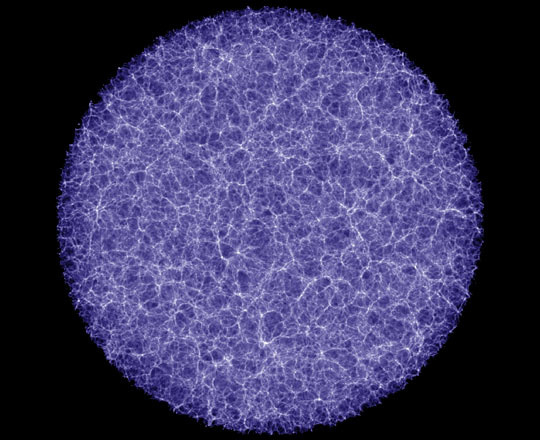
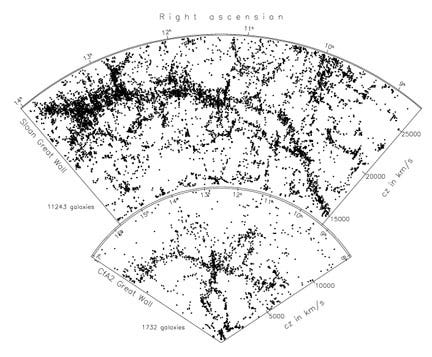


We don't know how to compute anything in an entangled world. So we invent a fiction of independent particles, so scientists have something they can work with.